6.3 Three-Dimensional Plotting Functions

The mesh function allows you to view a three dimensional object from various locations relative to the coordinate axes. The function mesh is described with help as:

>>  help mesh 
 
MESH 3-D mesh surface.
 
MESH(X,Y,Z,C) plots the colored parametric mesh defined by four matrix 
arguments.  The view point is specified by VIEW. The axis labels are 
determined by the range of X, Y and Z, or by the current setting of AXIS.
The color scaling is determined by the range of C, or by the current 
setting of CAXIS. The scaled color values are used as indices into the 
current COLORMAP.
 
MESH(X,Y,Z) uses C = Z, so color is proportional to mesh height.
 
MESH(x,y,Z) and MESH(x,y,Z,C), with two vector arguments replacing the 
first two matrix arguments, must have length(x) = n and length(y) = m 
where [m,n] = size(Z). In this case, the vertices of the mesh lines are 
the triples (x(j), y(i), Z(i,j)).
 
Note that x corresponds to the columns of Z and y corresponds to the rows.
 
MESH(Z) and MESH(Z,C) use x = 1:n and y = 1:m. In this case, the height,
Z, is a single-valued function, defined over a geometrically rectangular
grid.
 
MESH returns a handle to a SURFACE object.
 
AXIS, CAXIS, COLORMAP, HOLD, SHADING and VIEW set figure, axes, and surface
properties which affect the display of the mesh.
 
See also SURF, MESHC, MESHZ, WATERFALL. 

The function meshgrid used to produce data for three dimensional plots of functions is described by:

>>  help meshgrid
   
MESHGRID Generation of X and Y arrays for 3-D plots.
[X,Y] = MESHGRID(x,y) transforms the domain specified by vectors x and y
into arrays X and Y that can be used for the evaluation of functions of
two variables and 3-D surface plots.
The rows of the output array X are copies of the vector x and the columns
of the output array Y are copies of the vector y.
 
 

For example, to evaluate the function x*exp(-x^2-y^2) over the
rectangle:
-2 < x < 2, -2 < y < 2,
 
[X,Y] = meshgrid(-2:.2:2, -2:.2:2);
Z = X .* exp(-X.^2 - Y.^2);
mesh(Z)
 
[X,Y] = MESHGRID(x) is an abbreviation for [X,Y] = MESHGRID(x,x).

[X,Y,Z] = MESHGRID(x,y,z) produces packed 3-D arrays that can be used to
evaluate functions of three variables and 3-D volumetric plots.
 
See also SURF, SLICE.

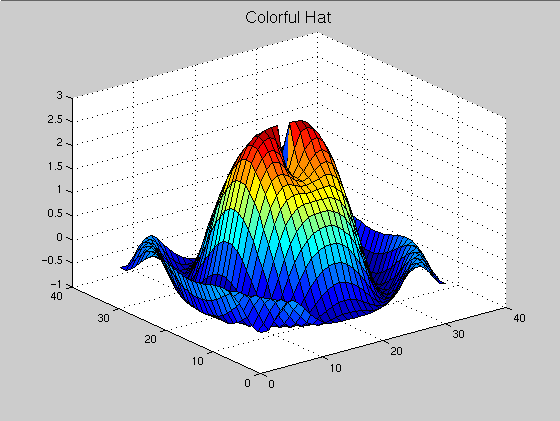
Here is a rather nice picture of a three dimensional object.

>>   [X,Y]=meshgrid(-1.5:.1:1.5,-1.5:.1:1.5);
 
>>   Z=sin(3*X.^2+2*Y.^2)./(X.^2+Y.^2);
        
 
Warning: Divide by zero.
>>   Z=sin(3*X.^2+2*Y.^2)./(X.^2+Y.^2+1e-10);
 
>>   mesh(Z)
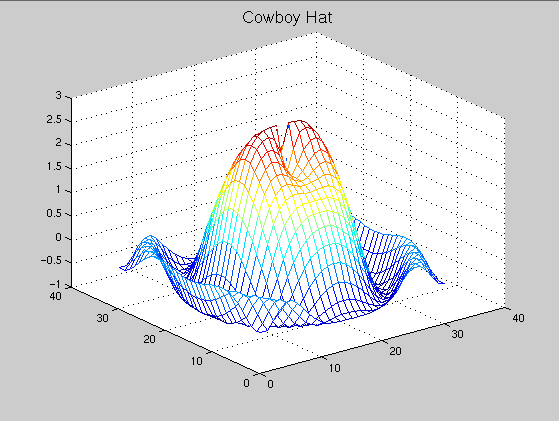
>>   ht=title('Cowboy Hat')
   
ht =
    6.0001
>>   set(ht,'FontSize',14)
 

Figure 6.7 Use of meshgrid and mesh

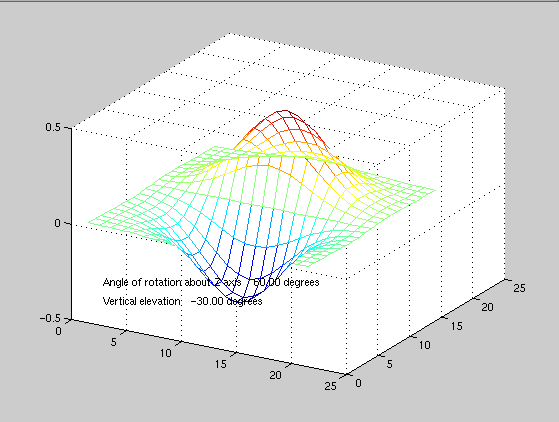
The function meshex allows the user to rotate an object about axes. It lists as:

Here is a session in which the example suggested in meshgrid help is seen from various points:

>> [x,y]=meshgrid(-2:.2:2,-2:.2:3);
 
>> z=x.*exp(-x.^2-y.^2);
 
>> mesh(z)

This showed the default position of the viewpoint. Now here is an example of 7 different views:

>> meshex(z,[0 0],[10 -5],7)

Here is the last view shown:

Figure 6.8 Another View of a Three Dimension Object

The surf command produces a three dimensional picture similar to the one from mesh. It is more colorful since each segment of the surface is colored rahter than just shown as a line. Here is the result of using surf on the same data used to make Figure 6.7.

Figure 6.9 Use of surf